Planning #
Parafoil problem #
To fly a well designed parafoil requires good understanding of its dynamics.
We start with the following assumptions:
- The parafoil is a point mass;
- Gravity is perfectly balanced by the lift force;
- The parafoil is steered by changing the heading angle of the parafoil;
- Wind remains constant at this early stage;
- x-y plane is the horizontal plane, z is the vertical direction;
- x is opposite to the direction of the wind, y is perpendicular to the wind direction;
- Target is at (0,0,0) for (x, y, z) coordinates;
- The touch down point relative velocity to the ground should be minimized.
Parafoil dynamics #
$$ \begin{cases} \dot{x} &= V_x = V \cos(\omega) - V_w\\ \dot{y} &= V_y = V \sin(\omega) \\ \dot{\omega} &= u \\ \end{cases} $$Flight time is determined by initial height and vertical velocity,
$$ T = \frac{H}{V_z} $$Optimal control #
The optimal control problem is to minimize the touch down point relative velocity to the ground. The cost function is defined as
$$ \begin{aligned} & \arg\min_u & \sqrt{V_x(T)^2 + V_y(T)^2} \\ & \text{s.t.} \\ & & |x(T)|^2 + |y(T)|^2 = 0 \end{aligned} $$Or equivalently, even more realistically,
$$ J = \arg\min_u |x(T)|^2 + |y(T)|^2 + \sqrt{V_x(T)^2 + V_y(T)^2 + V_z(T)^2} $$There should be normalizations for $x, y$, and vecolity residuals, to make the cost function dimensionless.
Discretization and dynamic programming #
When starting state and ending state are defined, the problem can be discretized and solved by dynamic programming. The state space is defined as
$$ \begin{aligned} & \mathcal{X} = \{x, y, \omega\} \\ & \mathcal{t} = \{t\} \end{aligned} $$接下来的开发可能会有一点点破坏性,所以新开一个分支来弄,不影响主分支的内容.
从目前阅读的内容看,DP主要的核心是把已经处理过的子问题的解存储起来,然后在需要的时候直接调用,而不是重新计算?
这让我觉得这里可能是不是需要用的是A*算法,而不是DP?
A*算法是一种启发式搜索算法,在搜索的时候,会根据当前的状态,通过一个启发函数来估计当前状态到目标状态的距离,然后根据这个距离来选择下一个状态,这样可以减少搜索的时间.
实际上,DP和A算法是有一定的关系的,DP是一种最优化的方法,而A算法是一种搜索的方法,在搜索的时候,可以使用DP来进行优化?
是不是需要看一下文献?
这个问题我可以再描述一下, 一个翼伞系统 $V,Vz,\bar{u}$ 从一个起点$x, y, H$ 开始滑翔, 在滑翔过程中,控制变量可以简化为 $\dot{\omega}$ , 即滑翔角度的变化, 这个控制实际上由双侧差动尾缘下拉来实现, 控制输入 $u = \dot{\omega} \in [-\bar{u}, \bar{u}]$. 同时,也应该知道翼伞本身是配平的,所以忽略 $z$ 方向的动力学, 只考虑 $x, y$ 平面内的动力学方程.
滑翔过程的目标是尽量减小着陆时与地面的相对速度,在考虑最简单的稳定风场时,这意味着要实现逆风着陆.
把着陆点定义为原点, 稳定风向定义为 $-x$ 轴方向, 考虑问题通用的解法,或者说一类问题的协调解法, 可能要形成如此的表格.
| $x_0$ | $y_0$ | $\omega_0$ | $H$ | $V$ | $V_z$ | $V_w$ | $\bar{u}$ | $T$ | $J$ | $u(t), t\in[0, T]$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 500 | 0 | 300 | 15 | 10 | 1 | 25 | 30 | ||
| 400 | 400 | 0 | 300 | 15 | 10 | 1 | 25 | 30 |
这里有几个有假设条件推出的事实.
- 翼伞飞行时间为 $T= \frac{H}{V_z}$, 这个是一个确定的值,不是一个变量.
- 着陆点的速度为 $V_x(T) = V \cos\omega(T) - V_w$, $V_y(T) = V \sin\omega(T)$.
- 翼伞最大飞行距离为 $V \cdot T$, 这个会和风速一起确定能够达到着陆点的起始范围, 这个问题本身就有一点点意思.
- 这个起始范围的不确定性也是相对容易解决的.
- 由 $\bar{u}$ 的存在, 翼伞的最小转弯半径也是有限的, 转弯半径 $r(t)=\frac{V}{\dot{\omega}}$的最小值为$\underset{\bar{}}{r} = V/\bar{u}$.
- 这样,上面的可行集合就可以看作是一个几何问题.
可行集合的分析 #
只考虑 $x, y$ 方向, 匹配起始的 $\omega_0$, 根据最远距离, 可以得到不等式:
$$ \sqrt{(x_0-V_w T)^2 + y_0^2} \le H \cdot \frac{V}{V_z} $$这是以 $(-V_w T, 0)$ 为圆心, $H \cdot \frac{V}{V_z}$ 为半径的圆. 在圆上的任何一点, 初始方位角必须为:
$$ \omega_0 = \arctan\frac{y_0}{x_0-V_w T} $$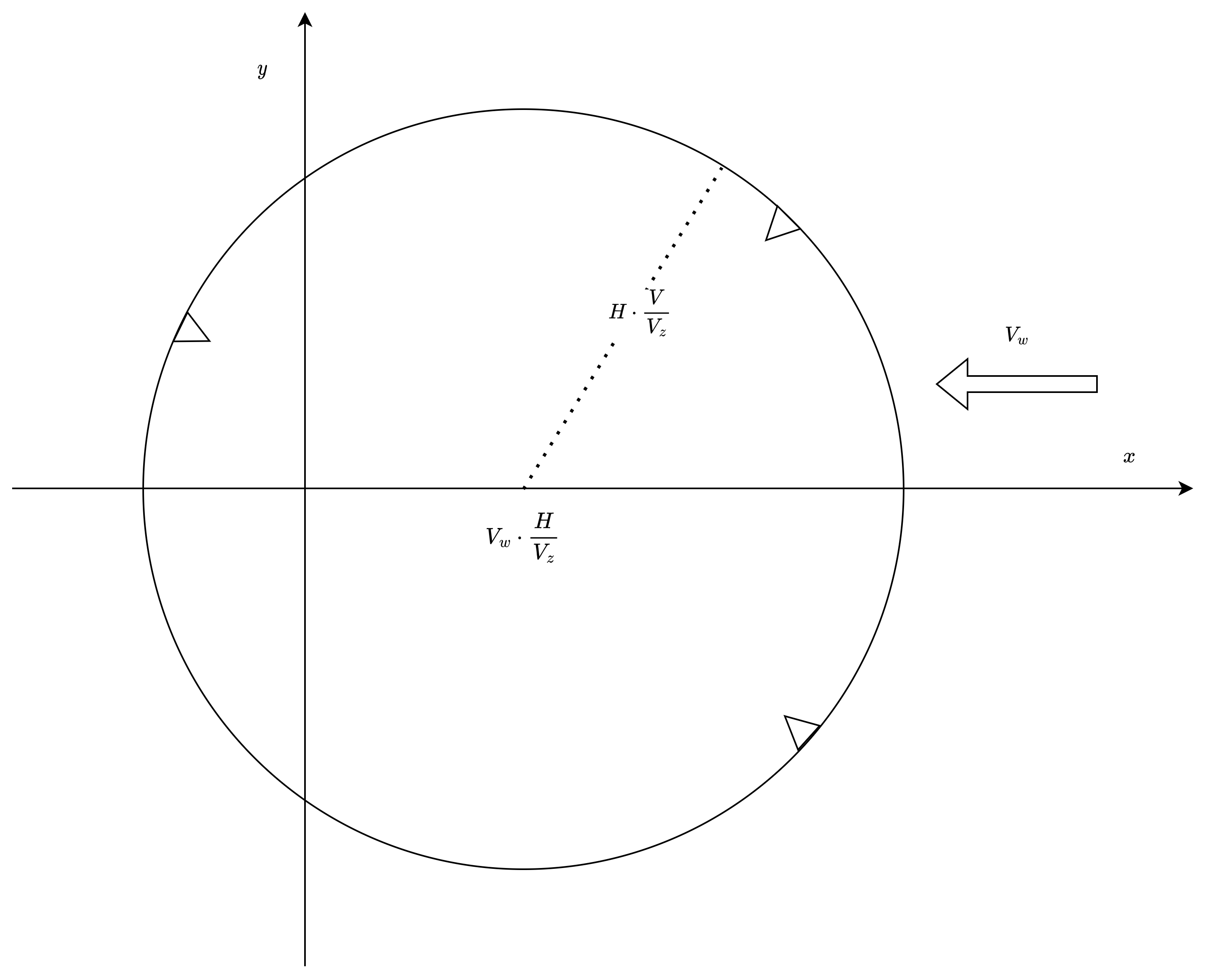
因此, 在考虑问题解的表格并试图进行轨迹规划问题综合时, 初始的可行集合为这个圆的内点. 我们还可以进一步求出每个内点对应的 $\omega_0$的允许范围, 通过求解最小转弯半径相关的几何问题.
这个集合问题的实质就是,一条由最小半径为 $\underset{\bar{}}{r}$ 的圆弧和直线线段组成的曲线, 连接 $(x_0, y_0)$ 和原点, 这个曲线的长度是 $V \cdot T$.
这个曲线起点的切线, 由 $\omega_0$确定.
几何分析 #
从某个点 $(x,y, \omega)$出发,可能到处两段圆弧,分别想两个方向, 对应于控制变量的 $\pm\bar{u}$, 在保持控制变量不变 $t$时间之后, 到达新的点 $(x', y', \omega')$, 这个过程可以看作是一个切线问题.

根据类似的几何分析,可以在 $(x,y,\omega)$构成的三维空间中,确定一个可行集合.
可达性的问题可能是一个挺难的问题 #
是否需要用Level Set方法来解决这个问题?
是否可以用Monte Carlo的方法来解决这个问题?
用Monte Carlo的方法怎么解?
如果只有三种控制, $-\bar{u}, \bar{u}, 0$, 那么这个问题就变成直线线段和圆弧组合的问题.
这个问题还可以这么提, 对于一个初始的位置, $x_0, y_0$, $\exists u(t)$, $x(T), y(T)$恰好到达原点吗? 考虑不考虑风场的情况.
所以说, 没有那么简单……
问题的复杂化和简化 #
那么从实际情况出发,能否对问题做出简化吗? 问题还有哪些复杂化的内容?
此外,还有一种要求就是, 必须从逆风的角度达到目标点, 这个问题还需要考虑.
此时我们应该从 $x, y, \omega = 0,0,0$ 出发, 由三段拼接
| 时间 | 线段类型 | 控制 | 起点 | 终点 |
|---|---|---|---|---|
| $t_3$ | 圆弧 | $\pm\bar{u}$ | $(0,0,0)$ | $(x_2, y_2, \omega_1)$ |
| $t_2$ | 直线 | 0 | $(x_2, y_2, \omega_1)$ | $(x_1, y_1, \omega_1)$ |
| $t_1$ | 圆弧 | $\pm\bar{u}$ | $(x_1, y_1, \omega_1)$ | $(x_0,y_0, \omega_0)$ |
并且有 $t_1 + t_2 + t_3 = T$
还有一个条件,就是 $0 \le t_1, t_3 < \frac{2\pi}{\bar{u}}$, 也就是周期性条件, 在当地转不超过一圈.
$$ \begin{aligned} &\omega_1=\pm\bar{u}t_1 \\ &\omega_0=\omega_1 \pm\bar{u}t_3 \end{aligned} $$这样可以实际上得到所有的可达集合. 整个设计条件的空间为:
$$ u_{t_3} \times t_3 \times t_1 \times u_{t_1} $$ $$ u_{t_i} = \{\bar{u}, -\bar{u}\}, t_i \in [0, \frac{2\pi}{\bar{u}}), i=1,3 $$这里只需要产生一个控制函数
$$ u(t_1, u_{t_1}, t_3, u_{t_3}) = t \mapsto \begin{cases} u_{t_1} & t \in (T-t_1, T] \\ 0 & t \in [t_3, T-t_1] \\ u_{t_3} & t \in [0, t_3) \end{cases} $$按照目前的微分方法, 从 $0, 0, 0$, 开始, 负向积分 $T = H/V_z$, 调用上面的控制函数,并且采用固定的风向函数, 就能得到一个轨迹.
问题进一步考虑 #
按照目前的程序, 能够分析出通过一个"转弯-直飞-转弯"序列达到目标点的可能起点状态, 这里要求的是逆风着陆.
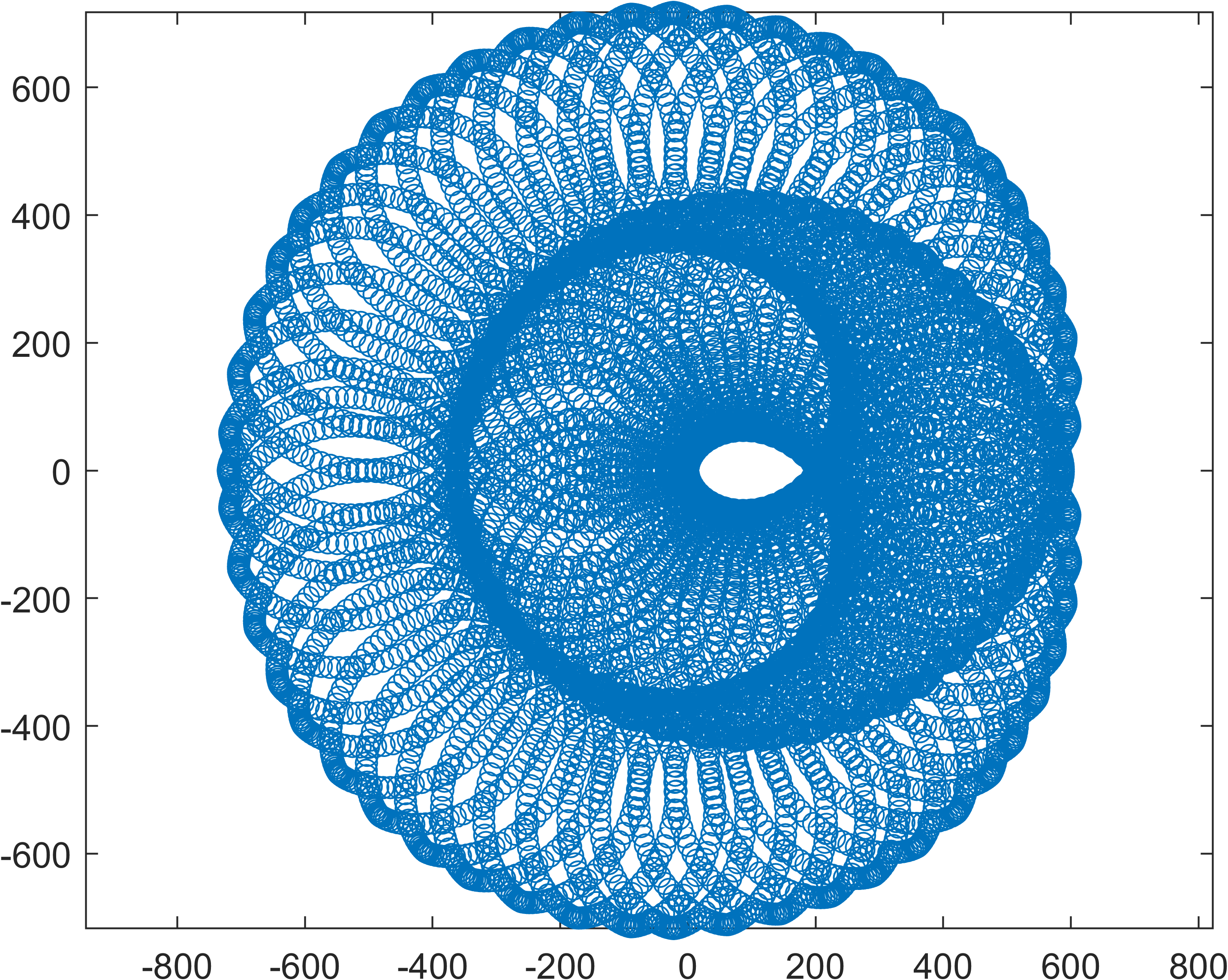
这是在风速 $1m/s$固定的情况下, 所有能够达到逆风着陆原点的起点的散点图.
如果把初始的 $\omega_0$作为 $z$坐标, 则由更意义的三维图像.
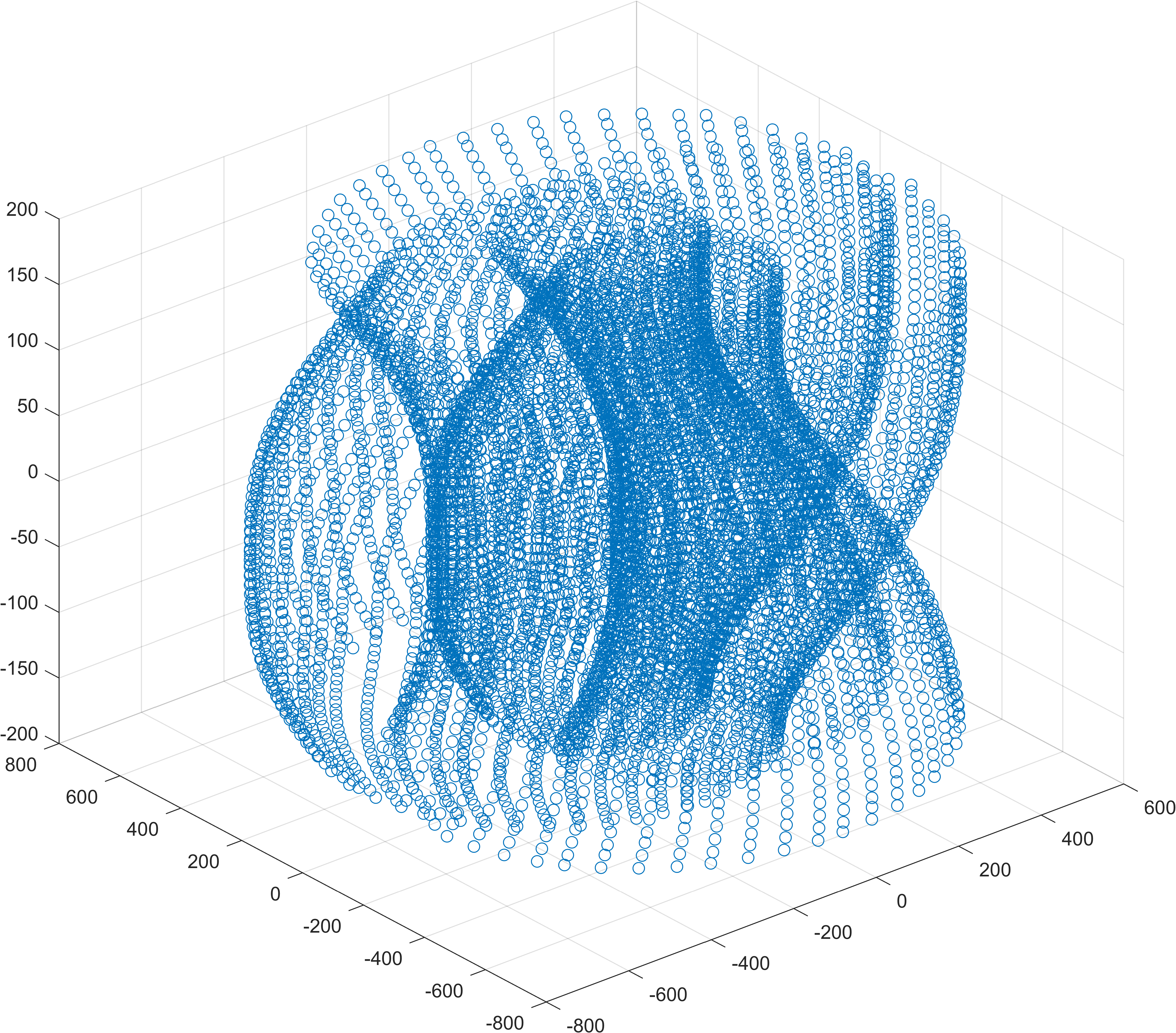
下一步 #
可以编译出多个可执行文件,通过参数来产生结果, 然后在Matlab中执行数值实验,对这个问题进行研究.
例如, “直飞-转弯(盘旋)-直飞-转弯"达到目标点的可能性, 这个集合是不是比前面那个集合小? 可能并不是. 允许盘旋是另外一个策略, 在盘旋之前做直飞又是另外一个策略.
一单具备微分方程的反演, 很多事情都是可能进行分析的.
这里有一个问题就是, 微分方程的正向积分和反向积分有什么关系?
这个还挺好玩的, 按照原则, 对于完美按照微分方程运行的系统而言,正向的积分和反向积分应该是可逆的? 那么什么样的系统是不可逆的呢?
这个问题可以从微分方程的解的唯一性来考虑, 也可以从物理的角度来考虑.
讨论 #
以上就是关于解的存在性的一点初步讨论, 是不是在某个方位内的所有起点 $x_0, y_0, \omega_0$都是存在一个几何路径呢? 特别是在风向固定, 控制变量取有限值的情况下?
那么, 控制变量取任意值的情况下, 这个可达的集合是不是有所变化呢?
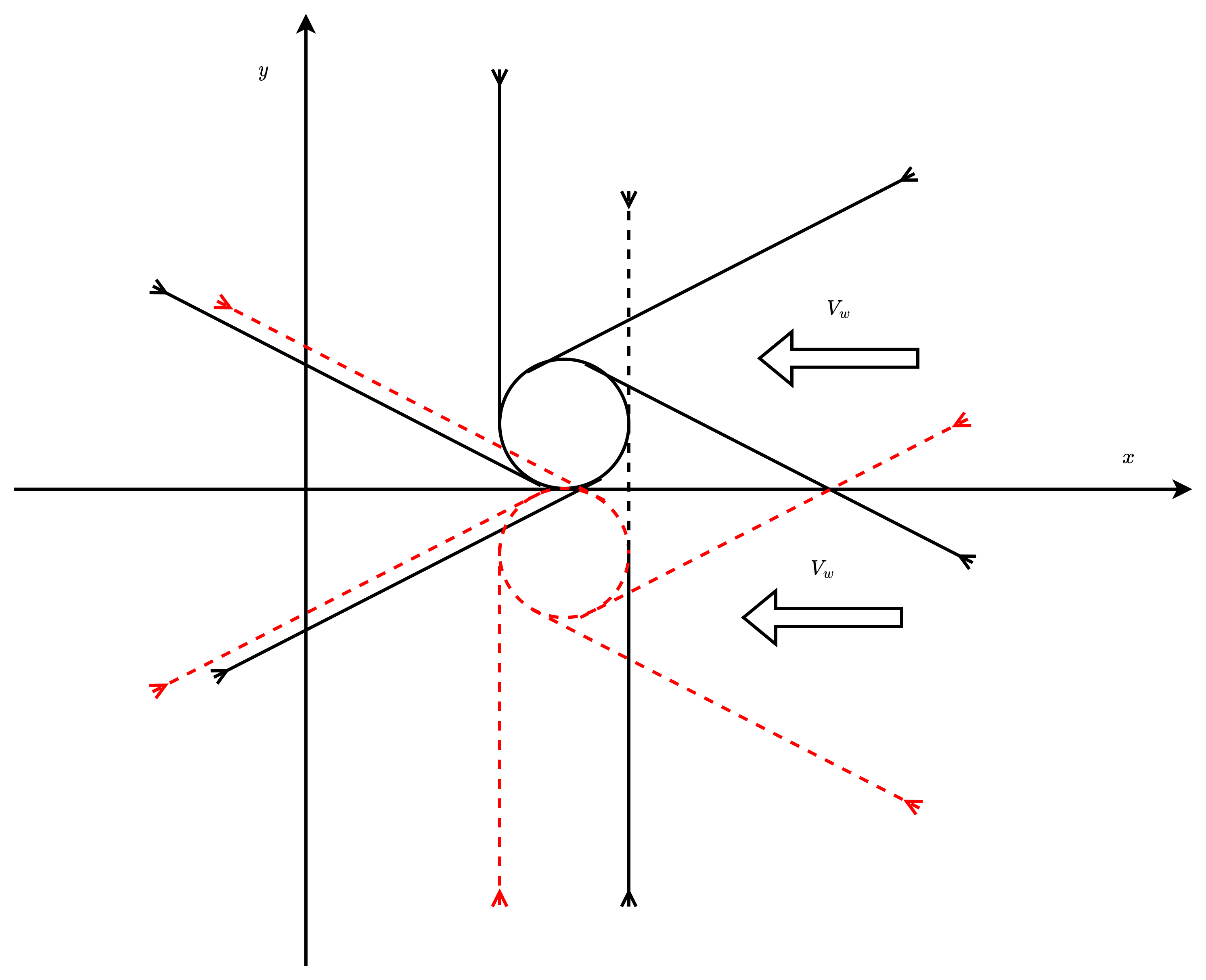
可达性 #
如果只考虑可达性的问题? 也就是说, 从一个起点, 通过一个控制函数, 能否到达目标点? 应该怎么解决这个问题呢?
$\mathcal{S}$的定义为:$\forall [x_0, y_0, \omega_0]^\mathtt{T} \in \mathcal{S}$, $\exists u(t), t\in[0, T], |u(t)|\le \bar{u}$, 使得$[x(T), y(T),\omega(T)]^\mathtt{T} = \mathbf{0}$.
要求出这个集合是不是一个挺有意思的问题? 这样马上就能判断出一个起点是否可达目标点.
或者,如果不能完美达到, 只能达到, 定义一个集合, $\mathcal{S}'$, $\mathcal{S}$的定义为:$\forall [x_0, y_0, \omega_0]^\mathtt{T} \in \mathcal{S}'$, $\exists u(t), t\in[0, T], |u(t)|\le \bar{u}$, 使得$[x(T), y(T)]^\mathtt{T} = \mathbf{0}$. 对这里着陆点的速度可以作为优化目标来考虑.
$$ J_{u(t), t\in[0, T]} = ||V_x(T)-Vw, V_y(T)||_2 $$这个问题的求解相对来说就容易多了?
再次考虑动态规划 #
这个问题按照动态规划的思路来表达.
对于一个给定的起点 $x_0, y_0, \omega_0$, 寻找 $u(t), t\in[0, T]$ 使得
$$ [x(T), y(T), \omega(T)]^\mathtt{T} = \mathbf{0} $$这个问题可以看作是一个动态规划问题, 从终点开始, 逆向求解.
问题变为, 对于一个给定的终点 $x(T), y(T), \omega(T)$, 寻找 $u(t), t\in[0, T-\Delta T]$, 使得
$$ [x(T-\Delta T), y(T-\Delta T), \omega(T-\Delta T)]^\mathtt{T} = \mathcal{S}_{T-\Delta T} \xleftarrow{u(t), t\in[T-\Delta T, T]} \mathcal{S} \equiv \mathbf{0} $$这里, 根据$u(t), t\in [T-\Delta T, T]$的选择, 可以得到一个新的状态 $\mathcal{S}_{T-\Delta T}$, 这个状态是一个集合, 也就是说, 从这个状态出发, 可以到达$\mathbf{0}$.
原来的问题, 就变成:
$$ \mathcal{S}_0 \xmapsto{u(t), t\in[0, \Delta T]} \mathcal{S}_{\Delta T} \xmapsto{u(t), t\in[\Delta T, 2\Delta T]} \cdots \xmapsto{u(t), t\in[T-\Delta T, T]} \mathcal{S}_T $$按照这个思路, 按照$\Delta T$来逐步对状态空间进行搜索, 并且把所有的中间解都存储起来.
状态的转换由前面实现的状态转换函数来实现. 如果我们把问题简化到控制变量只会取$0, -\bar{u}, \bar{u}$三种情况, 则最终是在如下的状态转移图中进行搜索.
stateDiagram
[*] --> S0
S0 --> S11 : $$ \mathbf{0}_{[0, \Delta T]}$$
S0 --> S12 : $$-\bar{u}_{[0, \Delta T]}$$
S0 --> S13 : $$\bar{u}_{[0, \Delta T]}$$
S11 --> S211 : $$ \mathbf{0}_{[\Delta T, 2\Delta T]}$$
S11 --> S212 : $$-\bar{u}_{[\Delta T, 2\Delta T]}$$
S11 --> S213 : $$\bar{u}_{[\Delta T, 2\Delta T]}$$
S12 --> S221 : $$ \mathbf{0}_{[\Delta T, 2\Delta T]}$$
S12 --> S222 : $$-\bar{u}_{[\Delta T, 2\Delta T]}$$
S12 --> S223 : $$\bar{u}_{[\Delta T, 2\Delta T]}$$
S13 --> S231 : $$ \mathbf{0}_{[\Delta T, 2\Delta T]}$$
S13 --> S232 : $$-\bar{u}_{[\Delta T, 2\Delta T]}$$
S13 --> S233 : $$\bar{u}_{[\Delta T, 2\Delta T]}$$
S222 --> ...
... --> S92
S91 --> S10 : $$ 0_{[T-\Delta T, T]}$$
S92 --> S10 : $$-\bar{u}_{[T-\Delta T, T]}$$
S93 --> S10 : $$\bar{u}_{[T-\Delta T, T]}$$
S10 --> [*]
大概分析一下全图搜索的复杂度, 从两头往中间搜索, 一共是 $N= \frac{T}{\Delta T}$ 个节点, 一共是 $2\cdot 3 ^{N/2}$.
这里会有两个问题, 第一个问题的复杂度太高, 第二个是, 这是一个打靶问题, 打靶本身就是一个我问题.
搜索的时候,两边往中间凑? 还是从怎么凑?
搜索的方法:
- 宽度优先搜索
- 深度优先搜索
- A*搜索
所以, 这里还有一个$\Delta T$的逐步减小的问题.
我们先来好好看看这个文献1中的动态规划是怎么做的.
首先是动力学方程, 同样采用简化的三自由度模型, 边界条件和目标函数的定义:
$$ J= \phi\left[ \mathbb{x}(t_f), t_f \right] + \int_{t_0}^{t_f} L\left[ \mathbb{x}(t), \phi_a(t), t\right] dt $$目标函数有两个部分组成, 一个部分是最终点, 一个部分是关于整个轨迹的积分.
边界条件是:
$$ \mathbb{x}(t_0) = \mathbb{x}_0, \mathbb{x}(t_f) = \mathbb{x}_f $$文章采用二次方来定义:
$$ \phi = (\tilde{\mathbb{x}}_f - \mathbb{x}_f)^\mathtt{T} \mathbf{P} (\tilde{\mathbb{x}}_f - \mathbb{x}_f) $$代价函数的定义为:
$$ J = (\tilde{\mathbb{x}}_f - \mathbb{x}_f)^\mathtt{T} \mathbf{P} (\tilde{\mathbb{x}}_f - \mathbb{x}_f) + \mathbb{u}^\mathtt{T} \mathbf{R} \mathbb{u} $$定义一个从当前位置到目标位置的最小代价函数:
$$ V(\mathbb{x}, t) = \min_{\mathbb{u}(t)}\left\{ \phi\left[ \mathbb{x}(t_f), t_f \right] + \int_{t}^{t_f} L\left[ \mathbb{x}(t), \phi_a(t), t\right] dt \right\} $$将时间$[0, t_f]$离散为$t_k = t_0 + k \Delta t$, $k=0,1,\cdots,K$, 并且 $k\Delta t = t_f - t_0$.
还应用网格精细化技术, 首先利用较粗的网格进行优化, 然后在局部进行网格细化.
BONACCORSI G, QUADRELLI M B, BRAGHIN F. Dynamic Programming and Model Predictive Control Approach for Autonomous Landings[J]. Journal of Guidance, Control, and Dynamics, 2022, 45(11): 2164-2173. DOI:10.2514/1.G006667. ↩︎